For any polynomial
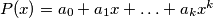
with integer coefficients, the number of odd coefficients is denoted by
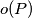
. For
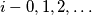
let
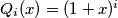
. Prove that if
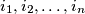
are integers satisfying
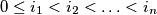
, then:
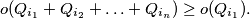
%V0
For any polynomial $P(x)=a_0+a_1x+\ldots+a_kx^k$ with integer coefficients, the number of odd coefficients is denoted by $o(P)$. For $i-0,1,2,\ldots$ let $Q_i(x)=(1+x)^i$. Prove that if $i_1,i_2,\ldots,i_n$ are integers satisfying $0\le i_1<i_2<\ldots<i_n$, then: $$o(Q_{i_1}+Q_{i_2}+\ldots+Q_{i_n})\ge o(Q_{i_1}).$$