Each of the numbers in the set
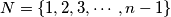
, where
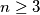
, is colored with one of two colors, say red or black, so that:
(i)

and
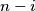
always receive the same color, and
(ii) for some
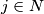
, relatively prime to

,

and
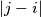
receive the same color for all
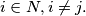
Prove that all numbers in

must receive the same color.
%V0
Each of the numbers in the set $N = \{1, 2, 3, \cdots, n - 1\}$, where $n \geq 3$, is colored with one of two colors, say red or black, so that:
(i) $i$ and $n - i$ always receive the same color, and
(ii) for some $j \in N$, relatively prime to $n$, $i$ and $|j - i|$ receive the same color for all $i \in N, i \neq j.$
Prove that all numbers in $N$ must receive the same color.