Let
be the interior of the circle
and let
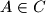
. Show that the function
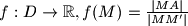
where
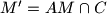
, is strictly convex; i.e.,
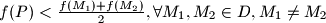
where
is the midpoint of the segment
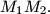
%V0
Let $D$ be the interior of the circle $C$ and let $A \in C$. Show that the function $f : D \to \mathbb R, f(M)=\frac{|MA|}{|MM'|}$ where $M' = AM \cap C$, is strictly convex; i.e., $f(P) <\frac{f(M_1)+f(M_2)}{2}, \forall M_1,M_2 \in D, M_1 \neq M_2$ where $P$ is the midpoint of the segment $M_1M_2.$
Školjka