Prove that for every point

on the surface of a regular tetrahedron there exists a point
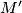
such that there are at least three different curves on the surface joining

to
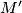
with the smallest possible length among all curves on the surface joining

to
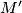
.
%V0
Prove that for every point $M$ on the surface of a regular tetrahedron there exists a point $M'$ such that there are at least three different curves on the surface joining $M$ to $M'$ with the smallest possible length among all curves on the surface joining $M$ to $M'$.