A sequence of polynomials
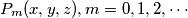
, in
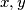
, and

is defined by
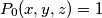
and by
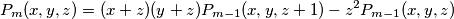
for
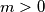
. Prove that each
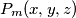
is symmetric, in other words, is unaltered by any permutation of
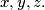
%V0
A sequence of polynomials $P_m(x, y, z), m = 0, 1, 2, \cdots$, in $x, y$, and $z$ is defined by $P_0(x, y, z) = 1$ and by
$$P_m(x, y, z) = (x + z)(y + z)P_{m-1}(x, y, z + 1) - z^2P_{m-1}(x, y, z)$$
for $m > 0$. Prove that each $P_m(x, y, z)$ is symmetric, in other words, is unaltered by any permutation of $x, y, z.$