A set of 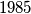 points is distributed around the circumference of a circle and each of the points is marked with
points is distributed around the circumference of a circle and each of the points is marked with  or
or 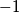 . A point is called “good” if the partial sums that can be formed by starting at that point and proceeding around the circle for any distance in either direction are all strictly positive. Show that if the number of points marked with
. A point is called “good” if the partial sums that can be formed by starting at that point and proceeding around the circle for any distance in either direction are all strictly positive. Show that if the number of points marked with 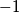 is less than
is less than 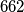 , there must be at least one good point.
, there must be at least one good point.
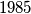 points is distributed around the circumference of a circle and each of the points is marked with
points is distributed around the circumference of a circle and each of the points is marked with  or
or 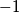 . A point is called “good” if the partial sums that can be formed by starting at that point and proceeding around the circle for any distance in either direction are all strictly positive. Show that if the number of points marked with
. A point is called “good” if the partial sums that can be formed by starting at that point and proceeding around the circle for any distance in either direction are all strictly positive. Show that if the number of points marked with 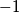 is less than
is less than 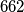 , there must be at least one good point.
, there must be at least one good point.  Školjka
Školjka