The tangents at
and
to the circumcircle of the acute-angled triangle
meet at
. Let
be the midpoint of
. Prove that
(a)
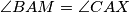
, and
(b)
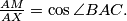
%V0
The tangents at $B$ and $C$ to the circumcircle of the acute-angled triangle $ABC$ meet at $X$. Let $M$ be the midpoint of $BC$. Prove that
(a) $\angle BAM = \angle CAX$, and
(b) $\frac{AM}{AX} = \cos\angle BAC.$
Školjka