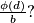Slični zadaci
Three persons  , are playing the following game:
, are playing the following game:
A -element subset of the set
-element subset of the set 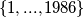 is randomly chosen, with an equal probability of each choice, where
is randomly chosen, with an equal probability of each choice, where  is a fixed positive integer less than or equal to
is a fixed positive integer less than or equal to 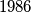 . The winner is
. The winner is 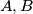 or
or  , respectively, if the sum of the chosen numbers leaves a remainder of
, respectively, if the sum of the chosen numbers leaves a remainder of 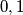 , or
, or  when divided by
when divided by  .
.
For what values of is this game a fair one? (A game is fair if the three outcomes are equally probable.)
is this game a fair one? (A game is fair if the three outcomes are equally probable.)
 , are playing the following game:
, are playing the following game:A
 -element subset of the set
-element subset of the set 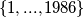 is randomly chosen, with an equal probability of each choice, where
is randomly chosen, with an equal probability of each choice, where  is a fixed positive integer less than or equal to
is a fixed positive integer less than or equal to 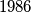 . The winner is
. The winner is 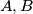 or
or  , respectively, if the sum of the chosen numbers leaves a remainder of
, respectively, if the sum of the chosen numbers leaves a remainder of 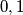 , or
, or  when divided by
when divided by  .
.For what values of
 is this game a fair one? (A game is fair if the three outcomes are equally probable.)
is this game a fair one? (A game is fair if the three outcomes are equally probable.)  The polynomial
The polynomial 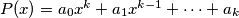 , where
, where 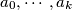 are integers, is said to be divisible by an integer
are integers, is said to be divisible by an integer  if
if  is a multiple of
is a multiple of  for every integral value of
for every integral value of  . Show that if
. Show that if  is divisible by
is divisible by  , then
, then 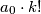 is a multiple of
is a multiple of  . Also prove that if
. Also prove that if 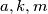 are positive integers such that
are positive integers such that 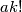 is a multiple of
is a multiple of  , then a polynomial
, then a polynomial  with leading term
with leading term 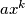 can be found that is divisible by
can be found that is divisible by 
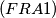 Let
Let  and
and  be two nonnegative integers. Denote by
be two nonnegative integers. Denote by 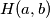 the set of numbers
the set of numbers  of the form
of the form 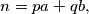 where
where  and
and  are positive integers. Determine
are positive integers. Determine 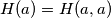 . Prove that if
. Prove that if 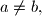 it is enough to know all the sets
it is enough to know all the sets 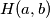 for coprime numbers
for coprime numbers 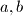 in order to know all the sets
in order to know all the sets 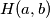 . Prove that in the case of coprime numbers
. Prove that in the case of coprime numbers  and
and 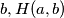 contains all numbers greater than or equal to
contains all numbers greater than or equal to 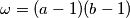 and also
and also 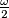 numbers smaller than
numbers smaller than 
 Školjka
Školjka 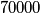 and each having more than
and each having more than 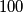 divisors.
divisors. 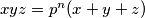 where
where 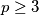 is a prime and
is a prime and 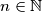 . Prove that the equation has at least
. Prove that the equation has at least 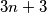 different solutions
different solutions 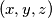 with natural numbers
with natural numbers 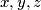 and
and 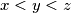 . Prove the same for
. Prove the same for 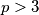 being an odd integer.
being an odd integer. 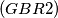 Let
Let 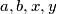 be positive integers such that
be positive integers such that  . Prove that the largest number not expressible in the form
. Prove that the largest number not expressible in the form 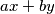 is
is 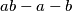 . If
. If 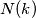 is the largest number not expressible in the form
is the largest number not expressible in the form 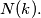
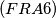 Consider the integer
Consider the integer 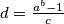 , where
, where  are positive integers and
are positive integers and 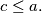 Prove that the set
Prove that the set  of integers that are between
of integers that are between  and relatively prime to
and relatively prime to 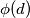 ) can be partitioned into
) can be partitioned into