From a collection of  persons
persons  distinct two-member teams are selected and ranked
distinct two-member teams are selected and ranked 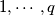 (no ties). Let
(no ties). Let  be the least integer larger than or equal to
be the least integer larger than or equal to 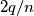 . Show that there are
. Show that there are  distinct teams that may be listed so that :
distinct teams that may be listed so that :
(i) each pair of consecutive teams on the list have one member in common and
(ii) the chain of teams on the list are in rank order.
Alternative formulation.
Given a graph with vertices and
vertices and  edges numbered
edges numbered 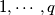 , show that there exists a chain of
, show that there exists a chain of  edges,
edges, 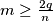 , each two consecutive edges having a common vertex, arranged monotonically with respect to the numbering.
, each two consecutive edges having a common vertex, arranged monotonically with respect to the numbering.
 persons
persons  distinct two-member teams are selected and ranked
distinct two-member teams are selected and ranked 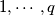 (no ties). Let
(no ties). Let  be the least integer larger than or equal to
be the least integer larger than or equal to 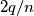 . Show that there are
. Show that there are  distinct teams that may be listed so that :
distinct teams that may be listed so that :(i) each pair of consecutive teams on the list have one member in common and
(ii) the chain of teams on the list are in rank order.
Alternative formulation.
Given a graph with
 vertices and
vertices and  edges numbered
edges numbered 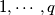 , show that there exists a chain of
, show that there exists a chain of  edges,
edges, 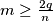 , each two consecutive edges having a common vertex, arranged monotonically with respect to the numbering.
, each two consecutive edges having a common vertex, arranged monotonically with respect to the numbering.  Školjka
Školjka