A particle moves from 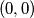 to
to 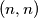 directed by a fair coin. For each head it moves one step east and for each tail it moves one step north. At
directed by a fair coin. For each head it moves one step east and for each tail it moves one step north. At 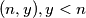 , it stays there if a head comes up and at
, it stays there if a head comes up and at 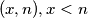 , it stays there if a tail comes up. Let
, it stays there if a tail comes up. Let be a fixed positive integer. Find the probability that the particle needs exactly
be a fixed positive integer. Find the probability that the particle needs exactly 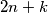 tosses to reach
tosses to reach 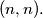
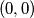 to
to 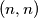 directed by a fair coin. For each head it moves one step east and for each tail it moves one step north. At
directed by a fair coin. For each head it moves one step east and for each tail it moves one step north. At 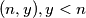 , it stays there if a head comes up and at
, it stays there if a head comes up and at 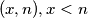 , it stays there if a tail comes up. Let
, it stays there if a tail comes up. Let be a fixed positive integer. Find the probability that the particle needs exactly
be a fixed positive integer. Find the probability that the particle needs exactly 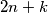 tosses to reach
tosses to reach 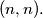
 Školjka
Školjka