The circle inscribed in a triangle

touches the sides
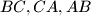
in
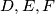
, respectively, and
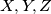
are the midpoints of
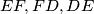
, respectively. Prove that the centers of the inscribed circle and of the circles around
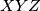
and

are collinear.
%V0
The circle inscribed in a triangle $ABC$ touches the sides $BC,CA,AB$ in $D,E, F$, respectively, and $X, Y,Z$ are the midpoints of $EF, FD,DE$, respectively. Prove that the centers of the inscribed circle and of the circles around $XYZ$ and $ABC$ are collinear.