Let
be a tetrahedron having each sum of opposite sides equal to
. Prove that
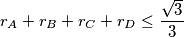
where
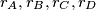
are the inradii of the faces, equality holding only if
is regular.
%V0
Let $ABCD$ be a tetrahedron having each sum of opposite sides equal to $1$. Prove that
$$r_A + r_B + r_C + r_D \leq \frac{\sqrt 3}{3}$$
where $r_A, r_B, r_C, r_D$ are the inradii of the faces, equality holding only if $ABCD$ is regular.
Školjka