Does there exist a second-degree polynomial
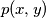
in two variables such that every non-negative integer

equals
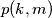
for one and only one ordered pair
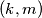
of non-negative integers?
Proposed by Finland.
%V0
Does there exist a second-degree polynomial $p(x, y)$ in two variables such that every non-negative integer $n$ equals $p(k,m)$ for one and only one ordered pair $(k,m)$ of non-negative integers?
Proposed by Finland.