Given five real numbers
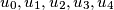
, prove that it is always possible to find five real numbers
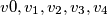
that satisfy the following conditions:
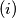
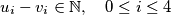
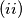
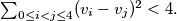
Proposed by Netherlands.
%V0
Given five real numbers $u_0, u_1, u_2, u_3, u_4$, prove that it is always possible to find five real numbers $v0, v_1, v_2, v_3, v_4$ that satisfy the following conditions:
$(i)$ $u_i-v_i \in \mathbb N, \quad 0 \leq i \leq 4$
$(ii)$ $\sum_{0 \leq i<j \leq 4} (v_i - v_j)^2 < 4.$
Proposed by Netherlands.