(a) Let
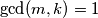
. Prove that there exist integers
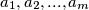
and
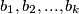
such that each product
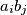
(
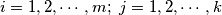
) gives a different residue when divided by
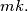
(b) Let
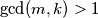
. Prove that for any integers
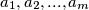
and
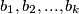
there must be two products
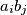
and
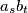
(
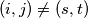
) that give the same residue when divided by
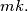
Proposed by Hungary.
%V0
(a) Let $\gcd(m, k) = 1$. Prove that there exist integers $a_1, a_2, . . . , a_m$ and $b_1, b_2, . . . , b_k$ such that each product $a_ib_j$ ($i = 1, 2, \cdots ,m; \ j = 1, 2, \cdots, k$) gives a different residue when divided by $mk.$
(b) Let $\gcd(m, k) > 1$. Prove that for any integers $a_1, a_2, . . . , a_m$ and $b_1, b_2, . . . , b_k$ there must be two products $a_ib_j$ and $a_sb_t$ ($(i, j) \neq (s, t)$) that give the same residue when divided by $mk.$
Proposed by Hungary.