Find the number of partitions of the set 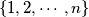 into three subsets
into three subsets 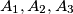 , some of which may be empty, such that the following conditions are satisfied:
, some of which may be empty, such that the following conditions are satisfied:
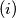 After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.
After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.
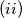 If
If 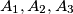 are all nonempty, then in exactly one of them the minimal number is even .
are all nonempty, then in exactly one of them the minimal number is even .
Proposed by Poland.
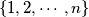 into three subsets
into three subsets 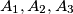 , some of which may be empty, such that the following conditions are satisfied:
, some of which may be empty, such that the following conditions are satisfied: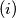 After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.
After the elements of every subset have been put in ascending order, every two consecutive elements of any subset have different parity.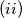 If
If 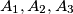 are all nonempty, then in exactly one of them the minimal number is even .
are all nonempty, then in exactly one of them the minimal number is even .Proposed by Poland.
 Školjka
Školjka