Slični zadaci
For each finite set  of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 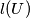 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 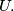 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 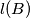 is greater than or equal to
is greater than or equal to 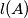 for each nonempty subset
for each nonempty subset  of
of 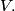
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set consisting of
consisting of 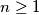 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 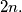
 of nonzero vectors in the plane we define
of nonzero vectors in the plane we define 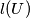 to be the length of the vector that is the sum of all vectors in
to be the length of the vector that is the sum of all vectors in 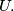 Given a finite set
Given a finite set  of nonzero vectors in the plane, a subset
of nonzero vectors in the plane, a subset  of
of  is said to be maximal if
is said to be maximal if 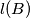 is greater than or equal to
is greater than or equal to 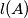 for each nonempty subset
for each nonempty subset  of
of 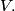
(a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively.
(b) Show that, for any set
 consisting of
consisting of 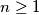 vectors the number of maximal subsets is less than or equal to
vectors the number of maximal subsets is less than or equal to 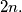
At a party attended by  married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques
married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques 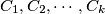 with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if
with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if 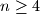 , then
, then 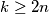 .
.
Proposed by USA.
 married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques
married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques 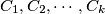 with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if
with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if 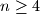 , then
, then 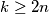 .
.Proposed by USA.
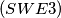 Find the natural number
Find the natural number  with the following properties:
with the following properties: Let
Let 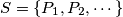 be an arbitrary finite set of points in the plane, and
be an arbitrary finite set of points in the plane, and 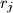 the distance from
the distance from 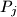 to the origin
to the origin 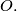 We assign to each
We assign to each 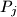 the closed disk
the closed disk 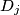 with center
with center 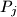 and radius
and radius 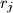 . Then some
. Then some  of these disks contain all points of
of these disks contain all points of 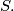
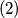
 is the smallest integer with the above property.
is the smallest integer with the above property.  Školjka
Školjka 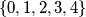 , if neighboring digits must differ by exactly one?
, if neighboring digits must differ by exactly one?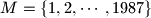 such that any arithmetic progression with
such that any arithmetic progression with  terms in the set
terms in the set  is not monochromatic.
is not monochromatic. 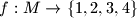 that is not constant on every set of
that is not constant on every set of 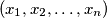 of the set
of the set 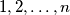 we call a pair
we call a pair 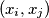 discordant if
discordant if 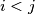 and
and 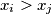 . Let
. Let 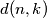 be the number of such permutations with exactly
be the number of such permutations with exactly  discordant pairs. Find
discordant pairs. Find 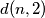 and
and 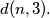
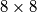 chessboard can be numbered by the numbers
chessboard can be numbered by the numbers 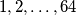 in such a way that the sum of the four numbers in each of its parts of one of the forms
in such a way that the sum of the four numbers in each of its parts of one of the forms