Let
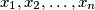
be real numbers satisfying
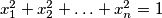
. Prove that for every integer
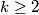
there are integers
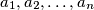
, not all zero, such that
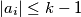
for all

, and
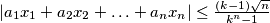
. (IMO Problem 3)
Proposed by Germany, FR
%V0
Let $x_1,x_2,\ldots,x_n$ be real numbers satisfying $x_1^2+x_2^2+\ldots+x_n^2=1$. Prove that for every integer $k\ge2$ there are integers $a_1,a_2,\ldots,a_n$, not all zero, such that $|a_i|\le k-1$ for all $i$, and $|a_1x_1+a_2x_2+\ldots+a_nx_n|\le{(k-1)\sqrt n\over k^n-1}$. (IMO Problem 3)
Proposed by Germany, FR