Prove that there exists a four-coloring of the set
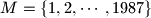
such that any arithmetic progression with

terms in the set

is not monochromatic.
Alternative formulation
Let
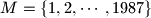
. Prove that there is a function
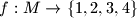
that is not constant on every set of

terms from

that form an arithmetic progression.
Proposed by Romania
%V0
Prove that there exists a four-coloring of the set $M = \{1, 2, \cdots, 1987\}$ such that any arithmetic progression with $10$ terms in the set $M$ is not monochromatic.
Alternative formulation
Let $M = \{1, 2, \cdots, 1987\}$. Prove that there is a function $f : M \to \{1, 2, 3, 4\}$ that is not constant on every set of $10$ terms from $M$ that form an arithmetic progression.
Proposed by Romania