Let
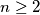
be an integer. Prove that if
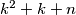
is prime for all integers

such that
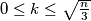
, then
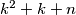
is prime for all integers

such that
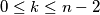
.(IMO Problem 6)
Original Formulation
Let
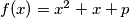
,
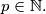
Prove that if the numbers
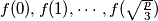
are primes, then all the numbers
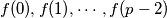
are primes.
Proposed by Soviet Union.
%V0
Let $n\ge2$ be an integer. Prove that if $k^2+k+n$ is prime for all integers $k$ such that $0\le k\le\sqrt{n\over3}$, then $k^2+k+n$ is prime for all integers $k$ such that $0\le k\le n-2$.(IMO Problem 6)
Original Formulation
Let $f(x) = x^2 + x + p$, $p \in \mathbb N.$ Prove that if the numbers $f(0), f(1), \cdots , f(\sqrt{p\over 3} )$ are primes, then all the numbers $f(0), f(1), \cdots , f(p - 2)$ are primes.
Proposed by Soviet Union.