Does there exist a function
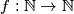
, such that
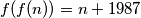
for every natural number
? (IMO Problem 4)
Proposed by Vietnam.
%V0
Does there exist a function $f : \mathbb N \to \mathbb N$, such that $f(f(n)) =n + 1987$ for every natural number $n$? (IMO Problem 4)
Proposed by Vietnam.
Školjka