Prove that for every natural number

(
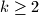
) there exists an irrational number

such that for every natural number

,
![[r^m] \equiv -1 \pmod k .](/media/m/d/5/1/d510b9e5f458d87ffc9b233c73986e46.png)
Remark. An easier variant: Find

as a root of a polynomial of second degree with integer coefficients.
Proposed by Yugoslavia.
%V0
Prove that for every natural number $k$ ($k \geq 2$) there exists an irrational number $r$ such that for every natural number $m$,
$$[r^m] \equiv -1 \pmod k .$$
Remark. An easier variant: Find $r$ as a root of a polynomial of second degree with integer coefficients.
Proposed by Yugoslavia.