The triangle

is inscribed in a circle. The interior bisectors of the angles
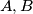
and

meet the circle again at
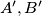
and
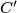
respectively. Prove that the area of triangle
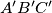
is greater than or equal to the area of triangle
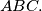
%V0
The triangle $ABC$ is inscribed in a circle. The interior bisectors of the angles $A,B$ and $C$ meet the circle again at $A', B'$ and $C'$ respectively. Prove that the area of triangle $A'B'C'$ is greater than or equal to the area of triangle $ABC.$