In a given tedrahedron
let
and
be the centres of edges
and
respectively. Prove that every plane that contains the line
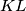
divides the tedrahedron into two parts of equal volume.
%V0
In a given tedrahedron $ABCD$ let $K$ and $L$ be the centres of edges $AB$ and $CD$ respectively. Prove that every plane that contains the line $KL$ divides the tedrahedron into two parts of equal volume.
Školjka