Let

be the greatest positive root of the equation
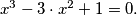
Show that
![\left[a^{1788} \right]](/media/m/2/0/b/20bbab2fd511dee40dec37fc2c138654.png)
and
![\left[a^{1988} \right]](/media/m/8/3/a/83a03eaaa1a03ce77e26e1535bddebfb.png)
are both divisible by 17. Here
![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png)
denotes the integer part of

%V0
Let $a$ be the greatest positive root of the equation $x^3 - 3 \cdot x^2 + 1 = 0.$ Show that $\left[a^{1788} \right]$ and $\left[a^{1988} \right]$ are both divisible by 17. Here $[x]$ denotes the integer part of $x.$