Let  be an acute-angled triangle. The lines
be an acute-angled triangle. The lines 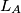 ,
, 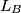 and
and 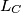 are constructed through the vertices
are constructed through the vertices  ,
,  and
and  respectively according the following prescription: Let
respectively according the following prescription: Let  be the foot of the altitude drawn from the vertex
be the foot of the altitude drawn from the vertex  to the side
to the side  ; let
; let 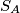 be the circle with diameter
be the circle with diameter 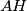 ; let
; let 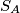 meet the sides
meet the sides  and
and  at
at  and
and  respectively, where
respectively, where  and
and  are distinct from
are distinct from  ; then let
; then let 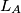 be the line through
be the line through  perpendicular to
perpendicular to  . The lines
. The lines 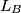 and
and 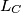 are constructed similarly. Prove that the lines
are constructed similarly. Prove that the lines 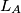 ,
, 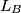 and
and 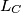 are concurrent.
are concurrent.
 be an acute-angled triangle. The lines
be an acute-angled triangle. The lines 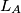 ,
, 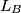 and
and 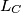 are constructed through the vertices
are constructed through the vertices  ,
,  and
and  respectively according the following prescription: Let
respectively according the following prescription: Let  be the foot of the altitude drawn from the vertex
be the foot of the altitude drawn from the vertex  to the side
to the side  ; let
; let 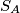 be the circle with diameter
be the circle with diameter 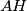 ; let
; let 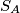 meet the sides
meet the sides  and
and  at
at  and
and  respectively, where
respectively, where  and
and  are distinct from
are distinct from  ; then let
; then let 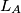 be the line through
be the line through  perpendicular to
perpendicular to  . The lines
. The lines 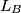 and
and 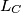 are constructed similarly. Prove that the lines
are constructed similarly. Prove that the lines 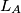 ,
, 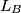 and
and 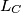 are concurrent.
are concurrent.  Školjka
Školjka