Let

be the centre of the inscribed circle of a triangle

Prove that for any point
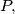
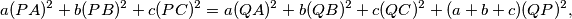
where
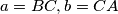
and
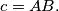
%V0
Let $Q$ be the centre of the inscribed circle of a triangle $ABC.$ Prove that for any point $P,$
$$a(PA)^2 + b(PB)^2 + c(PC)^2 = a(QA)^2 + b(QB)^2 + c(QC)^2 + (a + b + c)(QP)^2,$$
where $a = BC, b = CA$ and $c = AB.$