Let
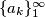
be a sequence of non-negative real numbers such that:
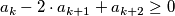
and
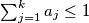
for all
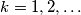
. Prove that:
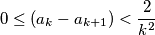
for all
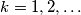
.
%V0
Let $\{a_k\}^{\infty}_1$ be a sequence of non-negative real numbers such that:
$$a_k - 2 \cdot a_{k + 1} + a_{k + 2} \geq 0$$
and $\sum^k_{j = 1} a_j \leq 1$ for all $k = 1,2, \ldots$. Prove that:
$$0 \leq (a_{k} - a_{k + 1}) < \frac {2}{k^2}$$
for all $k = 1,2, \ldots$.