Slični zadaci
There are n cars waiting at distinct points of a circular race track. At the starting signal each car starts. Each car may choose arbitrarily which of the two possible directions to go. Each car has the same constant speed. Whenever two cars meet they both change direction (but not speed). Show that at some time each car is back at its starting point.
Ali Barber, the carpet merchant, has a rectangular piece of carpet whose dimensions are unknown. Unfortunately, his tape measure is broken and he has no other measuring instruments. However, he finds that if he lays it flat on the floor of either of his storerooms, then each corner of the carpet touches a different wall of that room. He knows that the sides of the carpet are integral numbers of feet and that his two storerooms have the same (unknown) length, but widths of 38 feet and 50 feet respectively. What are the carpet dimensions?
 Školjka
Školjka 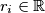 of the polynomial
of the polynomial 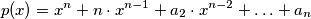 satisfying
satisfying 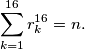
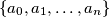 of real numbers satisfies the following conditions:
of real numbers satisfies the following conditions: 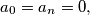
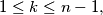
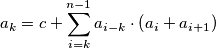
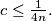
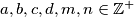 such that
such that 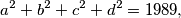
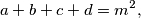 and the largest of
and the largest of 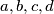 is
is 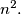 Determine, with proof, the values of
Determine, with proof, the values of  and
and 
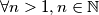 the equation
the equation 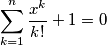 has no rational roots.
has no rational roots.