For a triangle
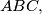
let

be its circumcircle with radius

The bisectors of the inner angles
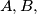
and

of the triangle intersect respectively the circle

again at points
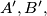
and
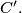
Prove the inequality
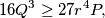
where

and

are the areas of the triangles
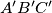
and

respectively.
%V0
For a triangle $ABC,$ let $k$ be its circumcircle with radius $r.$ The bisectors of the inner angles $A, B,$ and $C$ of the triangle intersect respectively the circle $k$ again at points $A', B',$ and $C'.$ Prove the inequality
$$16Q^3 \geq 27 r^4 P,$$
where $Q$ and $P$ are the areas of the triangles $A'B'C'$ and $ABC$ respectively.