Let
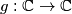
,
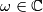
,
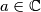
,
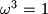
, and
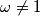
. Show that there is one and only one function
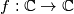
such that
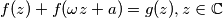
%V0
Let $g: \mathbb{C} \rightarrow \mathbb{C}$, $\omega \in \mathbb{C}$, $a \in \mathbb{C}$, $\omega^3 = 1$, and $\omega \ne 1$. Show that there is one and only one function $f: \mathbb{C} \rightarrow \mathbb{C}$ such that
$$f(z) + f(\omega z + a) = g(z),z\in \mathbb{C}$$