Let

and

be positive integers and let

be a set of

points in the plane such that
i.) no three points of

are collinear, and
ii.) for every point

of

there are at least

points of

equidistant from
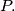
Prove that:
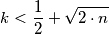
%V0
Let $n$ and $k$ be positive integers and let $S$ be a set of $n$ points in the plane such that
i.) no three points of $S$ are collinear, and
ii.) for every point $P$ of $S$ there are at least $k$ points of $S$ equidistant from $P.$
Prove that:
$$k < \frac {1}{2} + \sqrt {2 \cdot n}$$