Let
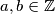
which are not perfect squares. Prove that if
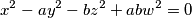
has a nontrivial solution in integers, then so does
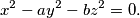
%V0
Let $a, b \in \mathbb{Z}$ which are not perfect squares. Prove that if $$x^2 - ay^2 - bz^2 + abw^2 = 0$$ has a nontrivial solution in integers, then so does $$x^2 - ay^2 - bz^2 = 0.$$
Školjka