Let
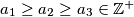
be given and let N
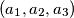
be the number of solutions
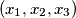
of the equation
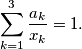
where
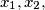
and
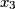
are positive integers. Prove that
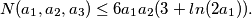
%V0
Let $a_1 \geq a_2 \geq a_3 \in \mathbb{Z}^+$ be given and let N$(a_1, a_2, a_3)$ be the number of solutions $(x_1, x_2, x_3)$ of the equation
$$\sum^3_{k=1} \frac{a_k}{x_k} = 1.$$
where $x_1, x_2,$ and $x_3$ are positive integers. Prove that $$N(a_1, a_2, a_3) \leq 6 a_1 a_2 (3 + ln(2 a_1)).$$
Školjka