The integer 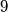 can be written as a sum of two consecutive integers:
can be written as a sum of two consecutive integers: 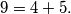 Moreover, it can be written as a sum of (more than one) consecutive positive integers in exactly two ways:
Moreover, it can be written as a sum of (more than one) consecutive positive integers in exactly two ways: 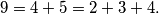 Is there an integer that can be written as a sum of
Is there an integer that can be written as a sum of 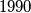 consecutive integers and that can be written as a sum of (more than one) consecutive positive integers in exactly
consecutive integers and that can be written as a sum of (more than one) consecutive positive integers in exactly 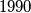 ways?
ways?
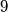 can be written as a sum of two consecutive integers:
can be written as a sum of two consecutive integers: 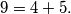 Moreover, it can be written as a sum of (more than one) consecutive positive integers in exactly two ways:
Moreover, it can be written as a sum of (more than one) consecutive positive integers in exactly two ways: 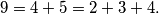 Is there an integer that can be written as a sum of
Is there an integer that can be written as a sum of 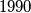 consecutive integers and that can be written as a sum of (more than one) consecutive positive integers in exactly
consecutive integers and that can be written as a sum of (more than one) consecutive positive integers in exactly 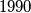 ways?
ways?  Školjka
Školjka