Given an initial integer 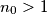 , two players,
, two players,  and
and  , choose integers
, choose integers 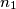 ,
, 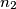 ,
, 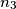 ,
,  alternately according to the following rules :
alternately according to the following rules :
I.) Knowing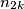 ,
,  chooses any integer
chooses any integer 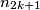 such that
such that
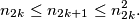
II.) Knowing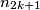 ,
,  chooses any integer
chooses any integer 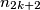 such that
such that
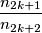
is a prime raised to a positive integer power.
Player wins the game by choosing the number 1990; player
wins the game by choosing the number 1990; player  wins by choosing the number 1. For which
wins by choosing the number 1. For which 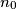 does :
does :
a.) have a winning strategy?
have a winning strategy?
b.) have a winning strategy?
have a winning strategy?
c.) Neither player have a winning strategy?
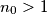 , two players,
, two players,  and
and  , choose integers
, choose integers 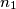 ,
, 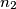 ,
, 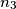 ,
,  alternately according to the following rules :
alternately according to the following rules : I.) Knowing
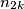 ,
,  chooses any integer
chooses any integer 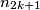 such that
such that 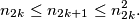
II.) Knowing
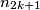 ,
,  chooses any integer
chooses any integer 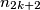 such that
such that 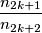
is a prime raised to a positive integer power.
Player
 wins the game by choosing the number 1990; player
wins the game by choosing the number 1990; player  wins by choosing the number 1. For which
wins by choosing the number 1. For which 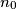 does :
does : a.)
 have a winning strategy?
have a winning strategy? b.)
 have a winning strategy?
have a winning strategy? c.) Neither player have a winning strategy?
 Školjka
Školjka