Let
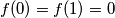
and
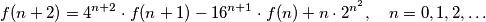
Show that the numbers
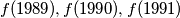
are divisible by
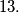
%V0
Let $f(0) = f(1) = 0$ and
$$f(n+2) = 4^{n+2} \cdot f(n+1) - 16^{n+1} \cdot f(n) + n \cdot 2^{n^2}, \quad n = 0, 1, 2, \ldots$$
Show that the numbers $f(1989), f(1990), f(1991)$ are divisible by $13.$