An eccentric mathematician has a ladder with  rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers
rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers  rungs of the ladder, and when he descends, each step he takes covers
rungs of the ladder, and when he descends, each step he takes covers  rungs of the ladder, where
rungs of the ladder, where  and
and  are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of
are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of 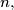 expressed in terms of
expressed in terms of  and
and 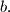
 rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers
rungs that he always ascends and descends in the following way: When he ascends, each step he takes covers  rungs of the ladder, and when he descends, each step he takes covers
rungs of the ladder, and when he descends, each step he takes covers  rungs of the ladder, where
rungs of the ladder, where  and
and  are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of
are fixed positive integers. By a sequence of ascending and descending steps he can climb from ground level to the top rung of the ladder and come back down to ground level again. Find, with proof, the minimum value of 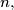 expressed in terms of
expressed in terms of  and
and 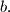
 Školjka
Školjka