Determine for which positive integers

the set
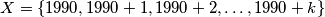
can be partitioned into two disjoint subsets

and

such that the sum of the elements of

is equal to the sum of the elements of
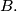
%V0
Determine for which positive integers $k$ the set $$X = \{1990, 1990 + 1, 1990 + 2, \ldots, 1990 + k\}$$ can be partitioned into two disjoint subsets $A$ and $B$ such that the sum of the elements of $A$ is equal to the sum of the elements of $B.$