Prove that there exists a convex 1990-gon with the following two properties :
a.) All angles are equal.
b.) The lengths of the 1990 sides are the numbers
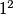
,
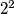
,
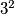
,

,
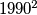
in some order.
%V0
Prove that there exists a convex 1990-gon with the following two properties :
a.) All angles are equal.
b.) The lengths of the 1990 sides are the numbers $1^2$, $2^2$, $3^2$, $\cdots$, $1990^2$ in some order.