Let
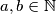
with
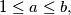
and
![M = \left[\frac {a + b}{2} \right].](/media/m/7/2/c/72cf1d082062d5caeb7a120b0b87a896.png)
Define a function
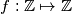
by
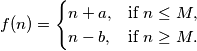
Let
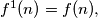
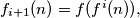
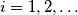
Find the smallest natural number

such that
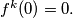
%V0
Let $a, b \in \mathbb{N}$ with $1 \leq a \leq b,$ and $M = \left[\frac {a + b}{2} \right].$ Define a function $f: \mathbb{Z} \mapsto \mathbb{Z}$ by
$$f(n) = \begin{cases} n + a, & \text{if } n \leq M, \\ n - b, & \text{if } n \geq M. \end{cases}$$
Let $f^1(n) = f(n),$ $f_{i + 1}(n) = f(f^i(n)),$ $i = 1, 2, \ldots$ Find the smallest natural number $k$ such that $f^k(0) = 0.$