Let  be a point inside a regular tetrahedron
be a point inside a regular tetrahedron  of unit volume. The four planes passing through
of unit volume. The four planes passing through  and parallel to the faces of
and parallel to the faces of  partition
partition  into 14 pieces. Let
into 14 pieces. Let 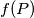 be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for
be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for 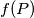 as
as  varies over
varies over 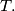
 be a point inside a regular tetrahedron
be a point inside a regular tetrahedron  of unit volume. The four planes passing through
of unit volume. The four planes passing through  and parallel to the faces of
and parallel to the faces of  partition
partition  into 14 pieces. Let
into 14 pieces. Let 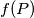 be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for
be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for 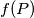 as
as  varies over
varies over 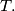
 Školjka
Školjka