Let

be a composite natural number and

a proper divisor of

Find the binary representation of the smallest natural number

such that
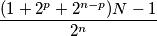
is an integer.
%V0
Let $n$ be a composite natural number and $p$ a proper divisor of $n.$ Find the binary representation of the smallest natural number $N$ such that
$$\frac{(1 + 2^p + 2^{n-p})N - 1}{2^n}$$
is an integer.