Na početku je u svaki od kvadrata raspoređenih kao na slici upisana nula.
![\setlength{\unitlength}{5pt}
\begin{center}
\begin{picture}(19, 19)
\newsavebox{\sq}
\savebox{\sq}(3, 3)[bl]{\put(0, 0){\line(1, 0){3}}\put(0, 3){\line(1, 0){3}}\put(0, 0){\line(0, 1){3}}\put(3, 0){\line(0, 1){3}}}
\newsavebox{\lih}
\savebox{\lih}(1, 1)[bl]{\put(0, 1.5){\line(1, 0){1}}}
\newsavebox{\liv}
\savebox{\liv}(1, 1)[bl]{\put(1.5, 0){\line(0, 1){1}}}
\multiput(0, 0)(4, 0){5}{\usebox{\sq}}
\multiput(0, 8)(4, 0){5}{\usebox{\sq}}
\multiput(0, 16)(4, 0){5}{\usebox{\sq}}
\multiput(0, 0)(0, 4){5}{\usebox{\sq}}
\multiput(8, 0)(0, 4){5}{\usebox{\sq}}
\multiput(16, 0)(0, 4){5}{\usebox{\sq}}
\multiput(3, 0)(4, 0){4}{\usebox{\lih}}
\multiput(3, 8)(4, 0){4}{\usebox{\lih}}
\multiput(3, 16)(4, 0){4}{\usebox{\lih}}
\multiput(0, 3)(0, 4){4}{\usebox{\liv}}
\multiput(8, 3)(0, 4){4}{\usebox{\liv}}
\multiput(16, 3)(0, 4){4}{\usebox{\liv}}
\end{picture}
\end{center}](/media/m/f/d/a/fda903c019fb506203b87263d6de69df.png)
U svakom potezu odabire se jedan od kvadrata te se istovremeno brojevi koji se nalaze u tom kvadratu i u svim njemu susjednim kvadratima uvećavaju za jedan.
Dokaži da je nakon određenog broja poteza:
a) moguće postići da u svakom kvadratu piše broj
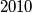
b) nemoguće postići da u svakom kvadratu piše broj
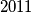
.
%V0
Na početku je u svaki od kvadrata raspoređenih kao na slici upisana nula.
$$$\setlength{\unitlength}{5pt}
\begin{center}
\begin{picture}(19, 19)
\newsavebox{\sq}
\savebox{\sq}(3, 3)[bl]{\put(0, 0){\line(1, 0){3}}\put(0, 3){\line(1, 0){3}}\put(0, 0){\line(0, 1){3}}\put(3, 0){\line(0, 1){3}}}
\newsavebox{\lih}
\savebox{\lih}(1, 1)[bl]{\put(0, 1.5){\line(1, 0){1}}}
\newsavebox{\liv}
\savebox{\liv}(1, 1)[bl]{\put(1.5, 0){\line(0, 1){1}}}
\multiput(0, 0)(4, 0){5}{\usebox{\sq}}
\multiput(0, 8)(4, 0){5}{\usebox{\sq}}
\multiput(0, 16)(4, 0){5}{\usebox{\sq}}
\multiput(0, 0)(0, 4){5}{\usebox{\sq}}
\multiput(8, 0)(0, 4){5}{\usebox{\sq}}
\multiput(16, 0)(0, 4){5}{\usebox{\sq}}
\multiput(3, 0)(4, 0){4}{\usebox{\lih}}
\multiput(3, 8)(4, 0){4}{\usebox{\lih}}
\multiput(3, 16)(4, 0){4}{\usebox{\lih}}
\multiput(0, 3)(0, 4){4}{\usebox{\liv}}
\multiput(8, 3)(0, 4){4}{\usebox{\liv}}
\multiput(16, 3)(0, 4){4}{\usebox{\liv}}
\end{picture}
\end{center}$$$
U svakom potezu odabire se jedan od kvadrata te se istovremeno brojevi koji se nalaze u tom kvadratu i u svim njemu susjednim kvadratima uvećavaju za jedan.
Dokaži da je nakon određenog broja poteza:
a) moguće postići da u svakom kvadratu piše broj $2010$
b) nemoguće postići da u svakom kvadratu piše broj $2011$.
![\setlength{\unitlength}{5pt}
\begin{center}
\begin{picture}(19, 19)
\newsavebox{\sq}
\savebox{\sq}(3, 3)[bl]{\put(0, 0){\line(1, 0){3}}\put(0, 3){\line(1, 0){3}}\put(0, 0){\line(0, 1){3}}\put(3, 0){\line(0, 1){3}}}
\newsavebox{\lih}
\savebox{\lih}(1, 1)[bl]{\put(0, 1.5){\line(1, 0){1}}}
\newsavebox{\liv}
\savebox{\liv}(1, 1)[bl]{\put(1.5, 0){\line(0, 1){1}}}
\multiput(0, 0)(4, 0){5}{\usebox{\sq}}
\multiput(0, 8)(4, 0){5}{\usebox{\sq}}
\multiput(0, 16)(4, 0){5}{\usebox{\sq}}
\multiput(0, 0)(0, 4){5}{\usebox{\sq}}
\multiput(8, 0)(0, 4){5}{\usebox{\sq}}
\multiput(16, 0)(0, 4){5}{\usebox{\sq}}
\multiput(3, 0)(4, 0){4}{\usebox{\lih}}
\multiput(3, 8)(4, 0){4}{\usebox{\lih}}
\multiput(3, 16)(4, 0){4}{\usebox{\lih}}
\multiput(0, 3)(0, 4){4}{\usebox{\liv}}
\multiput(8, 3)(0, 4){4}{\usebox{\liv}}
\multiput(16, 3)(0, 4){4}{\usebox{\liv}}
\end{picture}
\end{center}](/media/m/f/d/a/fda903c019fb506203b87263d6de69df.png)
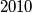
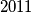 .
. ![\setlength{\unitlength}{5pt}
\begin{center}
\begin{picture}(19, 19)
\newsavebox{\sq}
\savebox{\sq}(3, 3)[bl]{\put(0, 0){\line(1, 0){3}}\put(0, 3){\line(1, 0){3}}\put(0, 0){\line(0, 1){3}}\put(3, 0){\line(0, 1){3}}}
\newsavebox{\lih}
\savebox{\lih}(1, 1)[bl]{\put(0, 1.5){\line(1, 0){1}}}
\newsavebox{\liv}
\savebox{\liv}(1, 1)[bl]{\put(1.5, 0){\line(0, 1){1}}}
\multiput(0, 0)(4, 0){5}{\usebox{\sq}}
\multiput(0, 8)(4, 0){5}{\usebox{\sq}}
\multiput(0, 16)(4, 0){5}{\usebox{\sq}}
\multiput(0, 0)(0, 4){5}{\usebox{\sq}}
\multiput(8, 0)(0, 4){5}{\usebox{\sq}}
\multiput(16, 0)(0, 4){5}{\usebox{\sq}}
\multiput(3, 0)(4, 0){4}{\usebox{\lih}}
\multiput(3, 8)(4, 0){4}{\usebox{\lih}}
\multiput(3, 16)(4, 0){4}{\usebox{\lih}}
\multiput(0, 3)(0, 4){4}{\usebox{\liv}}
\multiput(8, 3)(0, 4){4}{\usebox{\liv}}
\multiput(16, 3)(0, 4){4}{\usebox{\liv}}
\end{picture}
\end{center}](/media/m/f/d/a/fda903c019fb506203b87263d6de69df.png)
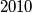
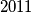 .
.  Školjka
Školjka