
is an acute-angled triangle.

is the midpoint of

and

is the point on

such that
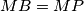
.

is the foot of the perpendicular from

to

. The lines through

perpendicular to
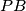
,
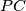
meet
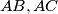
respectively at
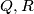
. Show that

is tangent to the circle through
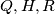
at

.
Original Formulation:
For an acute triangle
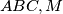
is the midpoint of the segment
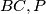
is a point on the segment

such that
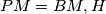
is the foot of the perpendicular line from

to
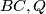
is the point of intersection of segment

and the line passing through

that is perpendicular to
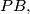
and finally,

is the point of intersection of the segment

and the line passing through

that is perpendicular to
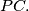
Show that the circumcircle of
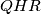
is tangent to the side

at point
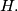
%V0
$ABC$ is an acute-angled triangle. $M$ is the midpoint of $BC$ and $P$ is the point on $AM$ such that $MB = MP$. $H$ is the foot of the perpendicular from $P$ to $BC$. The lines through $H$ perpendicular to $PB$, $PC$ meet $AB, AC$ respectively at $Q, R$. Show that $BC$ is tangent to the circle through $Q, H, R$ at $H$.
Original Formulation:
For an acute triangle $ABC, M$ is the midpoint of the segment $BC, P$ is a point on the segment $AM$ such that $PM = BM, H$ is the foot of the perpendicular line from $P$ to $BC, Q$ is the point of intersection of segment $AB$ and the line passing through $H$ that is perpendicular to $PB,$ and finally, $R$ is the point of intersection of the segment $AC$ and the line passing through $H$ that is perpendicular to $PC.$ Show that the circumcircle of $QHR$ is tangent to the side $BC$ at point $H.$
 is an acute-angled triangle.
is an acute-angled triangle.  is the midpoint of
is the midpoint of  and
and  is the point on
is the point on  such that
such that 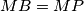 .
.  is the foot of the perpendicular from
is the foot of the perpendicular from  to
to  . The lines through
. The lines through  perpendicular to
perpendicular to 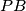 ,
, 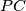 meet
meet 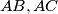 respectively at
respectively at 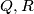 . Show that
. Show that  is tangent to the circle through
is tangent to the circle through 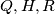 at
at  .
. 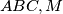 is the midpoint of the segment
is the midpoint of the segment 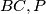 is a point on the segment
is a point on the segment  such that
such that 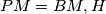 is the foot of the perpendicular line from
is the foot of the perpendicular line from  to
to 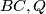 is the point of intersection of segment
is the point of intersection of segment  and the line passing through
and the line passing through  that is perpendicular to
that is perpendicular to 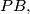 and finally,
and finally,  is the point of intersection of the segment
is the point of intersection of the segment  and the line passing through
and the line passing through  that is perpendicular to
that is perpendicular to 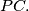 Show that the circumcircle of
Show that the circumcircle of 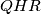 is tangent to the side
is tangent to the side  at point
at point 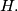
 Školjka
Školjka