Let  be any point on the circumscribed circle of
be any point on the circumscribed circle of 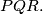 Then the feet of the perpendiculars from S to the three sides of the triangle lie on the same straight line. Denote this line by
Then the feet of the perpendiculars from S to the three sides of the triangle lie on the same straight line. Denote this line by 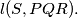 Suppose that the hexagon
Suppose that the hexagon 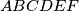 is inscribed in a circle. Show that the four lines
is inscribed in a circle. Show that the four lines 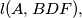
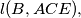
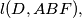 and
and 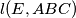 intersect at one point if and only if
intersect at one point if and only if 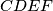 is a rectangle.
is a rectangle.
 be any point on the circumscribed circle of
be any point on the circumscribed circle of 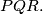 Then the feet of the perpendiculars from S to the three sides of the triangle lie on the same straight line. Denote this line by
Then the feet of the perpendiculars from S to the three sides of the triangle lie on the same straight line. Denote this line by 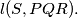 Suppose that the hexagon
Suppose that the hexagon 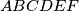 is inscribed in a circle. Show that the four lines
is inscribed in a circle. Show that the four lines 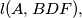
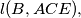
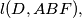 and
and 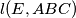 intersect at one point if and only if
intersect at one point if and only if 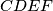 is a rectangle.
is a rectangle.  Školjka
Školjka