Let
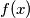
be a monic polynomial of degree
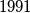
with integer coefficients. Define
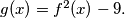
Show that the number of distinct integer solutions of
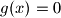
cannot exceed
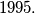
%V0
Let $f(x)$ be a monic polynomial of degree $1991$ with integer coefficients. Define $g(x) = f^2(x) - 9.$ Show that the number of distinct integer solutions of $g(x) = 0$ cannot exceed $1995.$