An infinite sequence
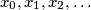
of real numbers is said to be bounded if there is a constant
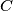
such that
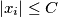
for every
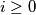
. Given any real number
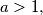
construct a bounded infinite sequence
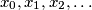
such that
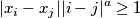
for every pair of distinct nonnegative integers
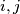
.
%V0
An infinite sequence $\,x_{0},x_{1},x_{2},\ldots \,$ of real numbers is said to be bounded if there is a constant $\,C\,$ such that $\, \vert x_{i} \vert \leq C\,$ for every $\,i\geq 0$. Given any real number $\,a > 1,\,$ construct a bounded infinite sequence $x_{0},x_{1},x_{2},\ldots \,$ such that
$$\vert x_{i} - x_{j} \vert \vert i - j \vert^{a}\geq 1$$
for every pair of distinct nonnegative integers $i, j$.