Consider 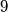 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
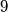 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.  Školjka
Školjka