Let
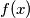
be a polynomial with rational coefficients and
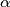
be a real number such that
![\alpha^3 - \alpha = [f(\alpha)]^3 - f(\alpha) = 33^{1992}.](/media/m/2/1/6/216d3c56b635fb22da2f4ad1fda4d7c5.png)
Prove that for each
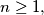
![\left [ f^{n}(\alpha) \right]^3 - f^{n}(\alpha) = 33^{1992},](/media/m/4/1/b/41bc0f447a9c314abc3b67cbc0dd14e5.png)
where
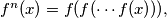
and

is a positive integer.
%V0
Let $f(x)$ be a polynomial with rational coefficients and $\alpha$ be a real number such that $$\alpha^3 - \alpha = [f(\alpha)]^3 - f(\alpha) = 33^{1992}.$$ Prove that for each $n \geq 1,$ $$\left [ f^{n}(\alpha) \right]^3 - f^{n}(\alpha) = 33^{1992},$$ where $f^{n}(x) = f(f(\cdots f(x))),$ and $n$ is a positive integer.